反射係数とは？～スミスチャートとの関係～（その１）

みなさん こんにちは。テクノシェルパ技術コンサルタントの河野です。

これまで”スミスチャートとは？～きちんと知ると便利です～”という6回のシリーズブログでスミスチャートについて紹介させていただきました。
今回はそのスミスチャートのさらに基礎となる反射係数について紹介させていただきます。

（当社の高周波（RF）コンサルサービスはこちら）

高周波の伝搬においては、インピーダンスの不整合により反射が発生します。海岸の防波堤を想像していただければいいのですが、防波堤より高い波が来た時には、防波堤を乗り越える波と防波堤から反射する波の二つに分かれます。
これと同様のことが高周波の伝搬でも発生します。

伝送線路の特性インピーダンスZ₀と負荷インピーダンスZ_Lの接続点で反射が発生する回路図で説明します。電源インピーダンス（Z_S Ω）から特性インピーダンス（Z₀ Ω）の線路を伝搬し、負荷インピーダンス（Z_L = R_L + jX_L Ω）に接続しています。

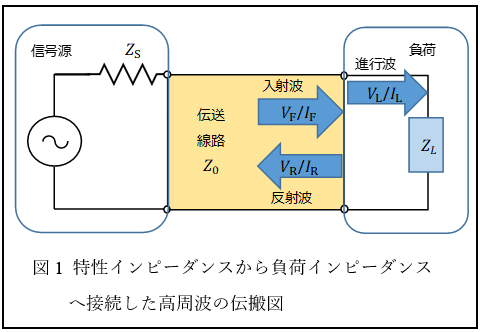
信号源から負荷に向かって伝搬する電磁波を入射波（電圧/電流をV_F/I_Fとします）といいます。また接続点から電源に向かって伝搬する電磁波を反射波(電圧/電流をV_R/I_Rとします)といいます。

そして、反射波と入射波の比を反射係数Γと呼びます。この値は、特に断りがない限り電圧の振幅で定義されます。そのときV_R = ΓV_F、I_R = －ΓI_Fとなります。

また、接続点から負荷インピーダンスに向かって伝搬する電磁波を進行波(電圧/電流をV_L/I_Lとします)といいます。

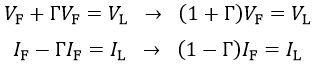
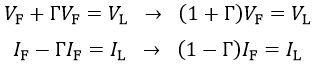
これらを辺々割り算すると

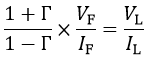
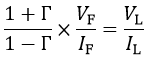
Z₀ = V_F/I_F、Z_L = V_L/I_Lなので、上式は次式となります。

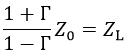
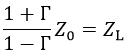
よって、反射係数Γは以下式で表されます。

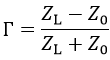
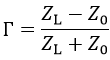
次に反射係数ΓとZ_Lの関係についてです。
まずはZ_Lの実数部（R_L）の大きさと反射係数Γの関係です。

(1) Z_L=∞ Ω（すなわちオープン）の場合、進行波（への入射波）はZ_Lで消費されずにすべて同相で反射されます。

したがってΓ=1となります。

(2) Z_L = 0 Ω（すなわちショート）の場合、進行波（Z_Lへの入射波）はZ_Lで消費されずにすべて逆相で反射されます。

したがってΓ=-1となります。

(3) Z_L = Z₀の場合、進行波（Z_Lへの入射波）はZ_Lですべて消費されるので反射波は発生しません。

したがってΓ=0となります。

続いて反射係数ΓとZ_Lの虚数部（jX_L）の関係を示します。

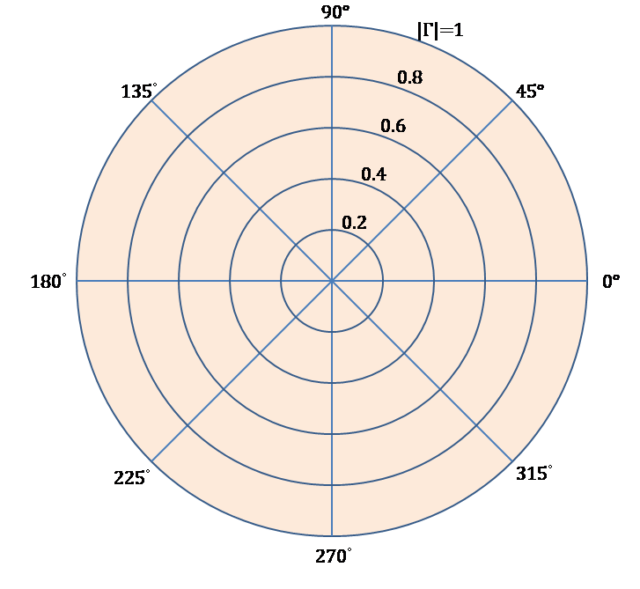
(4) Z_L = +jZ₀（誘導性）のとき、反射波は進行波に対して+90°の位相差で全反射します。

したがってΓ=+j1となります。

(5) Z_L = -jZ₀（容量性）のとき、反射波は進行波に対して-90°の位相差で全反射します。

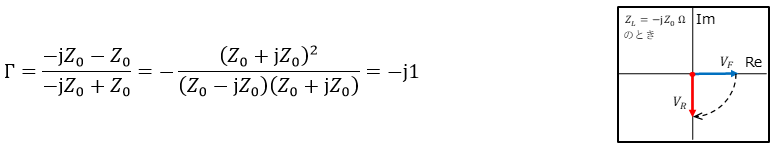
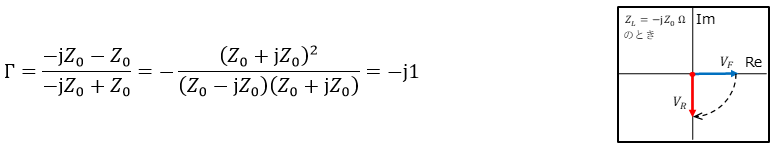
したがってΓ=－j1となります。

今回はここまでの説明とさせていただきます。次回はスミスチャートとの関係について解説させていただきます。次回をお楽しみに。

高周波・無線に関するブログやホームページは、下記からご覧いただけます。興味ある方は、ぜひ一度ご覧ください。

【関連リンク】

• テクノシェルパ 技術者教育サービス
• WTI　オンデマンド講座
• WTI　ライブ配信講座
• YouTube動画へのリンク（テクノシェルパ関連）

■技術者教育ブログ

• SSPA（Solid State Power Amplifier）の設計は機能ごとに分けて考えよう
• 分布定数回路とは？
• 同軸ケーブルの特性インピーダンスは任意に設定できるのか？
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その２）
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その３）
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その４）
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その５）
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その６）

■技術コンサルサービス

• 高周波（ＲＦ）コンサルサービス

■高周波・無線関連ページ

• 高周波(RF)・無線　設計受託
• 高周波電力増幅器開発
• 各種高周波部品開発
• 無線通信モジュール用アンテナ設計・評価受託
• 高周波マッチング工房
• 高周波開発インサイドストーリー

■高周波・無線関連ブログ

■電子回路設計 ヒントPLUS☆（高周波関連）

テクノシェルパ・メールマガジンの配信（無料）