反射係数とは？～スミスチャートとの関係～（その２）

みなさん こんにちは。テクノシェルパ技術コンサルタントの河野です。

前回 反射係数についてブログで紹介させていただきました。
今回はその反射係数とスミスチャートとの関係について紹介させていただきます。

（当社の高周波（RF）コンサルサービスはこちら）

前回のブログで反射係数Γと伝送線路の特性インピーダンスZ₀と負荷インピーダンスZ_Lの関係は次式であることを説明しました。

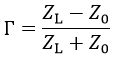
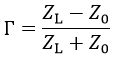
これを正規化インピーダンスz = Z_L / Z₀で書き直すとΓ = (z – 1) / (z + 1) となります。

正規化された負荷インピーダンス（z = r + jx Ω）と反射係数Γ = Γ_r + jΓ_i の関係は以下のとおりです。

ここで、実部、虚部それぞれ等しいので、次の2つの式が導出されます。

ここで(1)式を整理すると次式となり、rをパラタメータとした円の方程式となります。

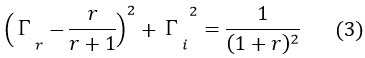
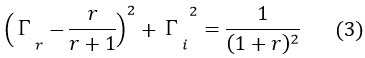
この(3)式において代表的なrと円の中心/半径の関係は以下の表になります。

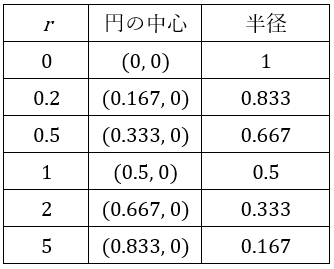
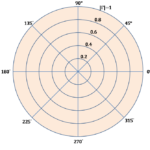
これらをグラフにすると図1となります。

どこかで見たことのあるグラフになりました。そうです。このrをパラタメータとした円がスミスチャートの等抵抗円なのです。

次に(2)式を整理すると次式となり、xをパラメータとした円の方程式となります。

この(4)式において代表的なxと円の中心/半径の関係は以下の表になります。

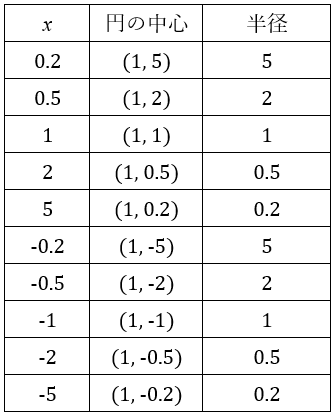
これらをグラフにすると図2となります。

反射係数|Γ|≦1なので、実際のグラフとしては、中心(0, 0)、半径１の円の内側のみ（赤線領域）となります。

これらxをパラメータとした円が、スミスチャートの等リアクタンス円となります。

こうして、図1と図２を合体させることでスミスチャートが完成します。
このようにインピーダンスと反射係数をスミスチャートで図示することが可能となるのです。

高周波・無線に関するブログやホームページは、下記からご覧いただけます。興味ある方は、ぜひ一度ご覧ください。

【関連リンク】

• テクノシェルパ 技術者教育サービス
• WTI　オンデマンド講座
• WTI　ライブ配信講座
• YouTube動画へのリンク（テクノシェルパ関連）

■技術者教育ブログ

• SSPA（Solid State Power Amplifier）の設計は機能ごとに分けて考えよう
• 分布定数回路とは？
• 同軸ケーブルの特性インピーダンスは任意に設定できるのか？
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その２）
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その３）
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その４）
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その５）
• ブログ・スミスチャートとは？ ～きちんと知ると便利です～（その６）
• ブログ・反射係数とは？～スミスチャートとの関係～（その１）

■技術コンサルサービス

• 高周波（ＲＦ）コンサルサービス

■高周波・無線関連ページ

• 高周波(RF)・無線　設計受託
• 高周波電力増幅器開発
• 各種高周波部品開発
• 無線通信モジュール用アンテナ設計・評価受託
• 高周波マッチング工房
• 高周波開発インサイドストーリー

■高周波・無線関連ブログ

■電子回路設計 ヒントPLUS☆（高周波関連）

テクノシェルパ・メールマガジンの配信（無料）